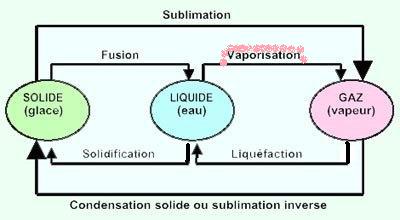
La vapeur : l'eau sous forme de gaz
Introduction.
Dans l’eau, les molécules sont liées les unes
aux autres par des liaisons hydrogène. Elles ont donc plus de
difficulté à passer dans la phase gazeuse car il faut
auparavant qu’elles aient acquis suffisamment
d’énergie pour rompre ces liaisons. Il faudra donc
dépenser plus d’énergie que si ces liaisons
n’existaient pas.
Nota : pour élever de 1°Celsius la température
d’une masse donnée d’eau, il faut dépenser 4
fois plus d’énergie que pour élever de
1°Celsius la température de la même masse
d’air, et 10 fois plus que pour élever de 1°Celsius
la température de la même masse de fer !
À une certaine température, dite température
d’ébullition, le liquide se mettra donc à
bouillir, laissant s’échapper quantité de
molécules dans l’atmosphère. Pour fondre la glace
d'eau, il en est de même : il faut d’abord que
l’énergie d’agitation des molécules soit
suffisante pour qu’un grand nombre de liaisons hydrogène
puissent être tordues.
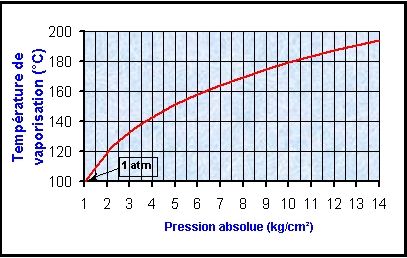
Par ailleurs, à chaque pression correspond une
température de vaporisation (production de
vapeur, transformation d'une substance liquide à l'état
de vapeur) déterminée.
Plus généralement (changement de
phase) :

Rappel : pression absolue = pression relative
(manométrique) + pression
atmosphérique.
-1 bar = 1,0197 kg/cm² = 100 000 Pa (ou
N/m²) = 0,987 atm = 750,06 mm Hg, ou 10,197 m CE
(colonne d'eau douce).
-1 kg/cm² = 0,980665 bar = 980,665 hPa. = 10 m CE = 735,56 mm
Hg.
Rappel des états physiques de l'eau en fonction de T [température] & P [pression] (diagramme de phases) :

Le point triple•
correspond au point de température et de pression ou
les trois phases solide/liquide/gazeuse
(glace/eau/vapeur) peuvent coexister d'une
manière stable, soit 273,16 K (0,01°C) sous 611 Pa (6,11
hPa) pour l'eau.
Le point critique correspond aux points de température
et de pression ou la différence entre liquide et gaz
disparaît :
L'air (lien
interne sur ce gaz) terrestre peut contenir de 0 à 7 %
de vapeur d'eau.
Sous la pression atmosphérique dite
"normale"* (1 atm ou
1013,25 hPa [ou 1 013,25
mbar] de pression absolue), la
température de vaporisation de l'eau, ou pression de
vapeur, est de 100°C (373,15 K); et
elle s'élève ou
s'abaisse quand la pression
augmente ou
diminue.
NB: la vapeur d'eau dans l'air fluctue entre 0,4 % et 4 %, et
est le principal gaz à effet de serre.
{*lien
interne explicatif}.
Par ailleurs :
La pression de vapeur saturante est est
la pression de vapeur maximale que l'atmosphère peut
supporter à une température donnée.
Cette pression saturante augmente avec la température
(s'exprime en Pascal [Pa] ) :
L'enthalpie spécifique de l'eau ou chaleur
sensible, est la quantité de chaleur contenue dans
1 kg d'eau, en fonction de la température donnée
(exprimée en kiloJoule par kg [kJ
kg-1] ).
La chaleur massique (ou spécifique) est la
quantité de chaleur nécessaire pour accroître la
température d'un degré Celsius par unité de
masse, donc pour 1 kg d'eau (exprimée en
kiloJoule par kg [kJ kg-1] ).
La chaleur volumique est la quantité de chaleur
nécessaire pour accroître la température d'un
degré Celsius, sur une unité de volume de 1 m3
d'eau (exprimée en kiloJoule par
m3 [kJ
m3-1]
).
|
|
|
ou Chaleur sensible |
Chaleur massique (ou spécifique ) |
|
|
|
|
kJ/kg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
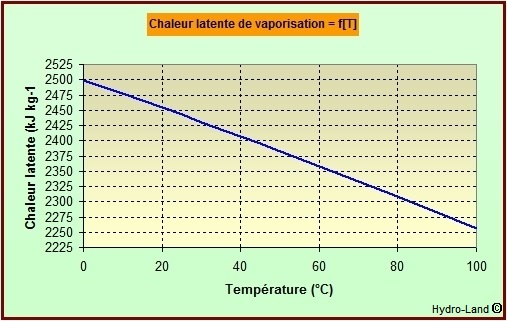
La chaleur latente de vaporisation
(CLvap)
est la quantité de chaleur nécessaire pour transformer
1 kg d'eau (et bouillante) en vapeur
sans changement de température - ou énergie thermique
nécessaire pendant le changement de l'état liquide
à l'état de vapeur (en kiloJoule
par kg [kJ
kg-1]
).
Elle est fonction de la pression : par exemple 2256,84 kJ kg sous
1013,25 hPa (pression atmosphérique
"normale").
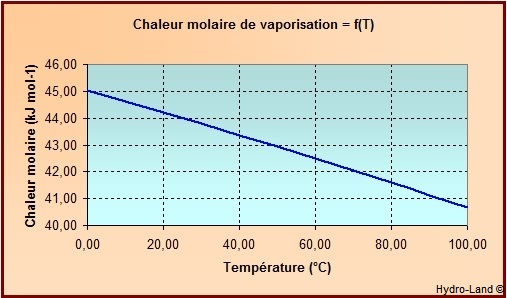
La chaleur molaire de vaporisation (DTvap,
ou enthalpie de vaporisation) est la chaleur
latente de vaporisation (à une
pression donnée) pour transformer 1 mole
(g
mol-1)
d'eau bouillante en vapeur (exprimée
en kiloJoule par mol,
kJ mol-1). C'est
donc le rapport : [chaleur latente de vaporisation]
/1000 g x [18,015
g].
Soit pour l'eau sous pression atmosphérique "normale" >
[2256,84 /1000 x 18,015] = 40,657 kJ
mol-1
ou 40 657 J
mol-1.
Nota : DTvap
représente le changement d'enthalpie pour la
variation H2O[liquide]
>>> H2O[gaz] ,
soit, DTvap
= Hgaz - Hliquide
L'enthalpie spécifique de la vapeur est la
chaleur totale contenue dans 1 kg de vapeur. C'est la somme
des enthalpies des différents états, liquide (eau) et
gazeux (vapeur). Elle s'exprime en kiloJoule par kg.
|
(hPa) |
- kJ kg-1 - |
°C |
- kJ mol-1 - |
- kJ kg-1 - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|


(suite).
Au sein de la vapeur d’eau l’agitation thermique
(mouvement incessant dont sont animés les
atomes ou molécules qui constituent la matière et ce
quel que soit l'état, gazeux, liquide ou solide dans lequel
elle se trouve) des molécules d’eau est grande :
elles se déplacent en tous sens, séparément les
unes des autres et de façon apparemment
désordonnée, défiant les lois de la pesanteur
car l’énergie thermique qui les habite est suffisamment
importante pour les empêcher de s’associer et de tomber
sous l’action de leur poids.
Un tel comportement est typique de tous les gaz, et donc
la vapeur d’eau peut être
considérée comme un gaz normal.
Rappel : la pression exercé par un gaz qui est en
équilibre avec son liquide est appelée pression
de vapeur à l'équilibre de ce liquide,
et elle augmente avec la température, et lorsque cette
pression de vapeur est égale à la pression
atmosphérique on atteint le point d'ébullition,
soit, sur notre globe, 1013,25 hPa (1 atm ou 101,325
kPa ) pour la pression atmosphérique dite "normale"
TPN (point d'ébullition = température
d'ébullition standard), de 100°C
(ou 313,15 K).
(rappel du terme
TPN et pages spéciales >
eb_salinite.htm
).
> ou à télécharger : programme
de calcul de l'ébullition en fonction de la pression
(feuille tableur, 49
ko).
Ci-joint un graphique donnant la pression de vapeur de l'eau,
à l'équilibre, en fonction de la température (en
°C) :
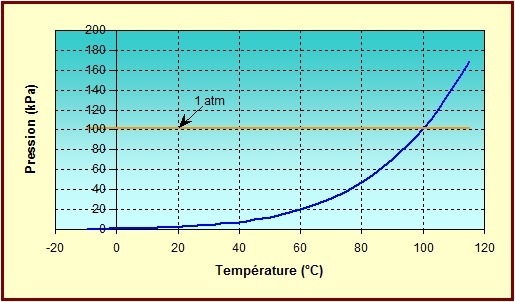
( kiloPascal, [1 kPa]
= 10 hectoPascal [10 hPa] )
Remarques.
Si nous exprimons la température en Kelvin (K) et la pression
en kPa, puis que nous construisons un graphique log P =
f(1/T).103,
de T= 273,15 K(0°C) et P=0,611 kPa,
à 388,15 K (115°C) et P=169,05
kPa, nous obtenons une droite :

l'équation de la droite est :
log10 P = a(1/T) + b ou plus
précisément avec nos valeurs > log P = -2,2573
(1/T.103) + 8,0647;
or, la pente de cette droite est fonction de la chaleur
molaire de vaporisation (DTvap)
:
avec, R = constante des gaz parfaits (8,314 J K-1 mol-1 ).
Les résultats donnent donc avec notre pente :
DTvap
= (-2,303 x 8,314 x (-2,2573.103) =
43 221 J mol-1 ou 43,22 kJ mol-1 pour
l'eau.
NOTA :
l'équation : ![]() est une forme de l'équation de Clausius-Clapeyron, et on peut
obtenir une autre forme pratique de l'équation, où P1
sera la pression de vapeur à la température T1 et P2
sera la pression de vapeur à T2 :
est une forme de l'équation de Clausius-Clapeyron, et on peut
obtenir une autre forme pratique de l'équation, où P1
sera la pression de vapeur à la température T1 et P2
sera la pression de vapeur à T2 : ![]() ,
,
Remarque : cette équation est une forme de l'équation
générale de Van't Hoff (lien
interne).
Cette expression permet donc :
Exemple 1 (sur
n°4) -
. Données : pression de vapeur de
l'éthanol (alcool
éthylique,
CH3-CH2-OH) =
47,01 kPa (P1) à 60°C
(T1), et avec une DTvap
= 4,22.104 J mol-1 (et R =
8,314 J K-1 mol-1),
. On calcule la température d'ébullition "normale" de
l'éthanol (T2) à 1 atm (P2=101,325
kPa) ?
. Calculs : T1 (60 + 273) = 333 K,
[1/T1 - 1/T2] =
log(P1/P2) /
[-DTvap/2,303R]
> donc, log(47,01/101,3) /
[-4,22.104/2,303.8.314)
= -1,51.10-4 k-1
et, [1/T2] = [1/T1] - 1,51.10-4
k-1 > [1/T2] = [1/333 K] -
1,51.10-4 = 2,852.10-3 et,
T2 (point d'ebullition de l'éthanol)
=350,63, ou ± 351 K, et Teb
(351-273) = 78°C
Exemple 2
(sur n°4) -
Estimation du point d'ébullition (Teb)
de l'eau au sommet du Mont
Blanc (4.808 m environ), sachant
que la pression atmosphérique à ce point est d'environ
555 hPa (55,5 kPa).
. Données : pression de vapeur de l'eau à 100°C
(T1) = 101,325 kPa
(P1), et DTvap
= 40,66 kJ mol-1 ou 40660 J mol-1, R = 8,314 J
K-1 mol-1 .
. Calculs : T1 (100 + 273,15) = 373,15 K,
[1/T1 - 1/T2] =
log(P1/P2) /
[-DTvap/2,303.R]
> donc, log(101,325/55,5) /
[-40660/2,303 x
8.314) = -1,231.10-4 k-1
donc, [1/T2] = [1/T1] - 1,231.10-4
k-1 > [1/T2] = [1/373 K] -
1,231.10-4 et, T2 = 356,76 K,
et Teb (356,76-273,15) =
83,6°C
Remarque : la même question au sommet de l'Everest
(plus haut sommet de la Terre, avec P= environ 32
kPa) donne Teb =
69,8°C.
(Nota : essayez donc de faire un œuf dur dans un
refuge de haute montagne à la pression du
lieu...[prévoir plutôt un autocuiseur !]
;
à noter que l'eau bout à 50°C
(soit moitié moins que la normale)
à une pression de 13,35 kPa (133,5 hPa), donc à environ
13,85 km d'altitude atmosphérique...
NOTES.
Comme pour tous les gaz, il est possible de comprimer la vapeur
d’eau, et inversement elle est expansible.
Rappel : le "gaz H2O" suit, pour
les faibles pressions et températures
élevées, les lois des gaz (cas du
gaz dilué approchant le gaz parfait),
> voir ce lien sur
les lois des gaz pour plus de précisions.
Exemples pour température T ou pression p constantes :
. à T constant > p1V1 =
p2V2,
donc :
2 m3 (V1) de
vapeur d'eau à 90°C sous une pression de 33 325 Pa
(p1), auraient sous une pression de 2000 Pa, et
à même température, un
volume V2 =
(p1V1)/p2, soit, (33
325 x 2)/2000 = 33,32 m3.
. à p constant > V1 / T1 =
V2/T2,
donc :
1,30 m3 (V1)
de vapeur d'eau à 100°C (373 K)
sous une pression constante, aurait à 250°C
(523 K), un volume de :
V2 =
(V1T2)/T1,
soit, (1,3 x 523)/373 = 1,82 m3.
L'équation d'état des gaz parfait (dans les conditions évoquées) pourrait aussi s'appliquer, soit :
avec n = nombre de moles et R = constante universelle
des gaz parfaits ( 8,314 472 J
mol-1
K-1 et
lien
externe).
Nota : R = L kPa
K-1
mol-1 ou
J
K-1
mol-1 ou m3
Pa mol-1
K-1) et
aussi 83,14472 L mbar mol-1
K-1,
. Exemple : supposons que 54 g de vapeur
(H2O gazeux) à 120°C se trouve
dans un contenant de 60 litres, et en supposant donc un comportement
de gaz idéal, on calcule la pression
p atteinte :
une mole H2O = 0,01801 kg/mole
(ou 18,01 g/mole), donc 54 g constituent donc
(54/18) = 3 moles (n), T : 120°C >
(120+273) = 393 K,
et,
soit donc une pression p de :
(3x8,314472x393)/60 =
163,38 kPa (ou 1,633
bar).
NB : si nous utilisons
l'équation de Van der Valls plus conforme à
la réalité des gaz (voir le
lien
interne sur l'équation) :
soit :  et donc p = [nRT / (V- nb)] -
[n² a / V²]
et donc p = [nRT / (V- nb)] -
[n² a / V²]
avec a = 553,7, b = 0,03049, n = 3,
nous obtenons p :
[(3x8,314472x393)/(60 - 3x0,03049)] -
[(3² x 553,7) / 60²] =
162,245 kPa (ou
1,622 bar).
Remarque : à noter l'écart de 1,135 kPa entre les deux
methodes (0,7 % environ) !
Lorsque l’on refroidit la vapeur d’eau,
l’agitation thermique des
molécules d’eau diminue.
Lorsque leur énergie d’agitation n’est plus
suffisante pour les en empêcher, les molécules
commencent à se lier les unes aux autres. Elles se rassemblent
en paquets pour finalement former, au sein de la vapeur d’eau,
des gouttes d’eau liquide qui tombent sous l'action de leur
poids.
La vapeur se transforme ainsi progressivement en
eau liquide (phénomène
dit, de liquéfaction).
Point de
rosée ou
Température de
rosée,
Tr (en anglais :
dew point temperature) :
C'est la température à partir de laquelle la vapeur
d'eau contenue dans de l'air humide commence à se condenser au
contact d'une surface froide.
Cette température dépend de la pression totale. Au
cours du refroidissement, l'humidité et la pression
partielle de la vapeur d'eau restent constantes.
Point de Tr, sous la pression atmosphérique dite "normale" [1013,25 hPa)
(avec T : température sèche, RH : humidité relative en %, Tr; calculs (en °C), à partir de la formule Magnus-Tetens,
- voir ci-dessous)
Nota : comme on le voit, le point de rosée (Tr) baisse en fonction de l'humidité relative (RH).
------------------ Calculs ----------------------------------------------------------------
Formule de HG Magnus-Tetens :
Domaine de validité :
![]() avec >
avec > ![]()
Nota : a = 17,27 et b = 237,7
[°C].
Formule de calcul approchée :
avec,
Graphe de la dépendance du point de rosée par rapport
à la température de l'air pour différents
niveaux d'humidité.
(fondé sur les approximations
d'A.Roche-Magnus).

(Source : Psychrometry and psychrometric charts - A W
T Barenbrug; Chamber of Mines of South Africa (1974)).
> Feuille de calcul (tableur) > programme calculTr.
NOTA : les
liaisons hydrogène peuvent exister dans la vapeur
d’eau, mais l’énergie d’agitation des
molécules y étant supérieure à
l'énergie de ces liaisons, les molécules ne peuvent
s’associer en grand nombre. Elles peuvent tout au plus
s’associer par deux ou par trois pour former ce que l’on
appelle des dimères ou des trimères.
La vapeur sursaturée peut exister à
l’état gazeux en dessous de
100°C, cet état est la
surfusion de
vapeur. Cet état se produit lorsque l'on refroidit la
vapeur rapidement, on peut dépasser le point de
liquéfaction (qui est le point d'ébullition de l'eau
vers 100°C), puis un dégagement de chaleur va se produire
(libération d'énergie de 2445 kJ par
kg, conditions
TPN) qui fait remonter la
température au voisinage de 100°C. Ce
phénomène prend un certain temps, d'où la
surfusion pendant ce délai :

Rappel de quelques propriétés de la
vapeur saturée.
NB : valeurs pour pression absolue = 1 kg/cm² (0,980665
bar) :
A noter aussi :
Éléments
thermodynamiques.
Principe de Le
Chatelier.
(voir éventuellement ces pages
spéciales)
Il peut s'énoncer ainsi : lorsqu'un système
à l'équilibre est soumis à une perturbation, il
réagit de manière à minimiser l'effet de la
perturbation.
Ainsi par exemple, de l'eau liquide et sa vapeur, sont maintenus dans
un contenant (par exemple dans un cylindre isolé et
fermé par un piston bien ajusté), la pression
étant donnée par un poids P
(schéma 1 suivant) :

A l'équilibre, la vitesse à laquelle l'eau se transforme en gaz (vapeur) est égale à la vitesse de transformation du gaz en liquide :
Si nous ajoutons de l'énergie thermique (de la chaleur) à ce système, une partie de l'eau s'évapore et se transforme en vapeur en absorbant de la chaleur, de sorte qu'il n'y a pas de hausse de température . En fait, après addition de chaleur nous dirons que, dans l'équation ci-dessus, l'équilibre c'est déplacé vers la droite, et nous observons plus de gaz et moins de liquide :

Par ailleurs, si nous refroidissons le
système (donc en retirant de la
chaleur), nous observons l'effet inverse : du gaz se
liquéfie et libère ainsi de l'énergie
(chaleur de liquéfaction) de sorte que
la température se maintient constante
(déplacement de l'équilibre vers la
gauche).
Un augmentation de pression ( compression adiabatique :
transformation effectuée sans qu'aucun transfert thermique
n'intervienne entre le système étudié et le
milieu extérieur) provoquerait aussi un déplacement de
l'équilibre, par exemple dans le schéma 2 ci-dessus, si
nous passons la pression initiale (soit p1) à la pression
augmentée (p2), nous voyons une diminution de volume du gaz
vapeur et une augmentation du volume du liquide : nous retrouvons le
schéma 1.
Mais des mesures précises montreraient que pour une diminution
de volume donné, la pression est inférieure à ce
qu'elle serait s'il n'y avait qu'un liquide ou un gaz seul
présent !
Cela est du à la différence de masse volumique entre
l'eau (env. 1000 kg
m3-1)
et la vapeur (env. 0,58 kg
m3-1)
: en g par g l'eau occupe moins de place que la vapeur et donc
l'équilibre [
chaleur
+
eau
<=>
vapeur
] se
déplace vers la gauche, la vapeur se transforme en eau liquide
et de la chaleur est dégagée. La chaleur ne pouvant
s'échapper la température augmente donc. En fait, le
système s'est déplacé le long de la courbe du
diagramme d'équilibre des phases de l'eau (courbe liquide-gaz)
:

A noter également : si nous ajoutons de la chaleur
à volume constant (par exemple schéma 1 mais en
bloquant le piston).
Dans ce cas l'addition de chaleur provoque l'évaporation d'une
certaine quantité d'eau, qui se transforme en vapeur en
absorbant de la chaleur, mais cette vapeur ne peut prendre de
l'expansion et la pression augmente. Le diagramme montre bien que
lorsque la pression est plus importante la température doit
l'être également pour que se maintienne
l'équilibre (le système s'est déplacé
vers le haut le long de la courbe liquide-gaz).
Ce qui est important : une partie de la chaleur fournie sert
à transformer l'eau en vapeur au lieu d'augmenter la
température du système. L'augmentation de
température est donc inférieure à celle qui
surviendrait si le système uniquement en un liquide, l'eau, ou
en un gaz, la vapeur, et n'était donc pas en
équilibre.
Transformation de l'eau en vapeur sans
ébullition (voir schéma ci-après -
échelle déformée) :

Soit donc, par exemple, de nous rendre du point A (phase liquide)
au point D (vapeur) sans passer par l'ébullition (augmentation
de la température à pression constante), pour ce faire
nous "contournerons" le point critique
p.
Méthode : nous somme au point A sous forme liquide
(température env.110°C (383 K) et
sous pression env.6 MPa (9,8 atm)
) puis nous augmentons la pression
jusqu'au point B (à température constante) , puis nous
augmentons la température jusqu'au point C (à pression
constante) au-delà de la température critique, puis
enfin nous baissons la pression jusqu'au point D (à
température constante).
Ceci est vraiment possible grâce à la continuité
des états liquides et gazeux, et au-delà du point
critique les différences de propriétés
disparaissent.
Sous une pression inférieure à la pression
atmosphérique il existe une correspondance entre tension
de vapeur (pression) et température. Mais lorsqu'on chauffe un
récipient, une tuyauterie ou une chaudière, contenant
de l'eau sous une pression supérieure à la
pression atmosphérique, et que la température
de cette eau s'élève, on dit que l'eau est
chaude tant que sa température n'atteint pas 100
°C. On dit qu'elle est surchauffée, ou mieux :
chaude et surpressée aux températures
supérieures.
Quand on vaporise de l'eau, dans une chaudière par exemple,
les bulles de vapeur formées dans la masse de liquide,
montent, crèvent le plan d'eau et se dégagent dans la
chambre de vapeur en entraînant avec elles une petite
quantité d'eau (eau vésiculaire), qui peut
rester liquide du fait du très faible diamètre des
gouttes (la tension superficielle de la goutte s'ajoute à la
pression ambiante).
Le titre de la vapeur est le rapport (en %) du poids de vapeur
au poids de l'eau liquide coexistants dans un volume
déterminé.
Le titre de la vapeur saturée produite par une
chaudière, dépend de beaucoup d'éléments,
notamment des impuretés de l'eau, de la pression, du poids de
vapeur dégagée par m d'eau et par heure, etc.
Il atteint couramment 97 % et parfois moins, aussi est-il souvent
utile de prévoir un sécheur à la sortie
de la chaudière. Quand le titre de la vapeur saturée
est 100 %, on dit que la vapeur est sèche. Elle est
humide dans le cas contraire.
II est possible d'obtenir, sous une pression déterminée
P, de la vapeur surchauffée, c'est-à-dire
à une température supérieure à la
température de vaporisation correspondant à P, mais
pour cela il faut la soustraire au contact de l'eau liquide.
Certaines chaudières sont équipées à cet
effet d'un faisceau surchauffeur, nécessairement distinct du
vaporisateur.
Pour transformer 1 kg d'eau liquide à 0 °C, en
vapeur saturée à la pression P, il faut lui fournir les
calories suivantes :
Nota : ces grandeurs varient avec la pression..........![]()
Enfin, pour obtenir de la vapeur surchauffée, il faut fournir
à la vapeur saturée une quantité de chaleur
supplémentaire appelée chaleur de
surchauffe.
On trouvera ci-après, la chaleur totale de vaporisation et de
surchauffe pour quelques pressions et températures :

A noter que la chaleur totale de vaporisation (et chaleur totale
de vaporisation et de surchauffe) sont égales à l'
enthalpie* de la vapeur.
|
* L enthalpie (H) est définie par la somme de
l'énergie interne d'un système (U) et du
produit de la pression (P) par le volume (V). Soit, H = U +
PV. |
NB - le zéro des échelles correspond à l'eau
liquide, à la température de la glace fondante, sous
une pression atmosphérique normale, soit 1013 millibars ou 760
mm Hg.
Les pressions sont en pression absolue (pression
relative - manomètrique- + pression atmosphérique, en
kg/cm²), les températures en °C.
La courbe en trait fort correspond à la courbe de saturation.
Rappel : 1 kcal=4,1855
kJ.
Ce graphique permet de résoudre certain problème -
exemples :
|
|