Hydrostatique - Exemples (calculs)
Raccourcis :
PRESSION EN UN POINT D'UNE PAROI D'UN RÉCIPIENT OUVERT
Château d'eau
& conduites
Forces sur tube
immergé et bouché

VASES COMMUNICANTS

Deux vases communicants ont respectivement S1 =100 cm2 et S2 = 6400 cm2 de section carrée.
Ils contiennent de l'eau et sont fermés par deux pistons en contact avec l'eau.

On exerce sur le plus petit piston une force totale F1 de 200 N (20,39 kgf).




Calculons la force totale F2 qu'il faut exercer sur l'autre piston pour que l'on ait équilibre :
La force F1 crée une surpressionDp qui se transmet dans tous le liquide.

On a donc :

Dp = F1/S1 = F2/S2

et,
F2 = (F1 x S2) /S1

ou avec les valeurs :

F2 = (200 x 6400) / 100, soit :  F2 = 12 800 N (ou 1305,2 kgf ou 1,3 tonne-force)

Nota : ou une pression de (12800/0,64) = 20 000 Pa (N/m² )



-







PRESSION EN UN POINT D'UNE PAROI D'UN RÉCIPIENT OUVERT

1 - Soient deux récipients A et B, remplis d'eau de mer (avec Mv = 1027 kg . m-3) :

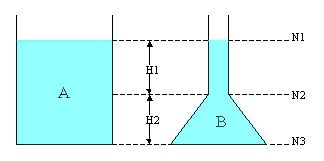
  • pression atmosphérique P0 : 102 000 Pa (1020 hPa ou 1020 mbar),
  • g = 9,81 m.s²
  • H1 = 0,5 m,
  • H2 = 0,4 m.




On calculera :

  1. les pressions totales p1, p2, p3 qui s'exercent en des points intérieurs au liquide, dans les deux récipients, aux niveaux N1, N2, N3,
  2. les pressions qui s'exercent sur les parois en des points se trouvant aux mêmes niveaux que précédemment, dans les deux récipients,

Résultats :
1 - On a les mêmes valeurs dans les deux récipients, car la pression ne dépend que de la hauteur de liquide :

En N1 (surface du liquide) : p1 = P0 = 102 000 Pa

En N2 : p2 = Mv .g .H1 + P0 , soit, (1027 x 9,81 x 0,5) + 102 000 Pa = 107 037,43 Pa
ou 1070,37 hPa (10,914 m de CE).

En N3 : p3 = Mv.g (H1+H2) + P0 , soit, (1027 x 9,81 x (0,5+0,4) + 102 000 Pa ,
= 111 067,38 Pa ou 1110,67 hPa (11,325 m de CE).




2 - La pression atmosphérique n'intervient pas :

En N1 (surface du liquide) : p1 = P0 = 0 Pa

En N2 : p2 = Mv .g .H1 , soit, (1027 x 9,81 x 0,5) = 5037,43 Pa
ou 50,37 hPa (0,514 m de CE).

En N3 : p3 = Mv.g (H1+H2) , soit, (1027 x 9,81 x (0,5+0,4) = 9067,38 Pa,
ou 90,67 hPa (0,924 m de CE).











2 - Soient, un château d'eau et sa conduite principale de longueur L :
(eau du circuit de distribution : Mv = 999,7 kg . m-3, pour T°C = 10)


Résultats :
Pression en N : en surface, seule la pression atmosphérique compte, soit donc P0 = 101 325 Pascals, ou encore 1,033 kg/cm².

Pression en N1 : la pression ne dépend que de la hauteur de liquide , donc, (999,7 x 9,81 x 20) = 196 141 Pa ou 1 961 hPa (2 kg/cm² environ).

Pression en N2 : la pression ne dépend que des hauteurs soient H1 + H2 , donc, (999,7 x 9,81 x (20+5)) = 245 176 Pa ou 2 451 hPa (2,5 kg/cm²) ).

Pression en N3 : H3 = (50 x SIN 11°55) = 10 m, la pression ne dépend que des hauteurs soient,
H1 + H2 + H3 , donc, (999,7 x 9,81 x (20+5+10)) = 343 247 Pa ou 3 432 hPa (3,5 kgf/cm²).

-







On place à une extrémité d'un tube cylindrique une plaque de section 20 cm² et pesant 316 g.
On plonge le tout dans de l'eau : Mv = 999,7 kg.m-3,

On calculera la profondeur minimale h, ou il faut placer l'extrémité inférieure afin que la plaque reste collée à l'embouchure du tube ?

.

 


Résultats :
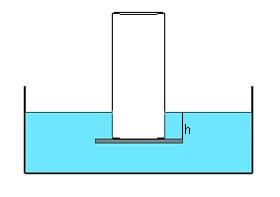
Pour que la plaque reste collée, il faut que la somme des forces appliquées vers le haut soit plus grande que la somme de celles appliquées vers le bas; ou au minimum qu'elles soient égales.

Forces vers le bas : force due à la pression atmosphérique + poids de la plaque.
Forces vers le haut : force due à la pression atmosphérique + force due à la profondeur d'immersion h,
Donc la force due à la pression atmosphérique étant dans les deux sens s'annule, donc il reste :

Donc, mg = Mv g h S, d'ou > h = mg / (Mvg S) > h = m / (Mv S) , soit :
h = (0,316 / (999,7 x 0,002)) = 0,158 m ou 15,8 cm de profondeur d'immersion.


Fin du chapitre Calcul d'hydrostatique